这是之前朋友出的一道题目,感觉不错,就拿来分享一下。
问题如下:
一个单向链表,怎么判断他是否存在环?
图示:
对于最简单的做法就是:
用一个指针走一圈,如果重复遇到其他任何一个指针,则证明有环。
但是这样做的问题就是:
单指针需要留下脚印,会弄脏链表数据,而如果不能脏数据的话,就需要增加一个容器,并且增加查找的开销。
有没有更好的方法呢?有的,定义一对快慢指针分别为ptr_fast,ptr_slow,ptr_slow走一步,ptr_fast走两步,如果ptr_slow和ptr_fast最终能相遇,那么证明有环。
解释如下:
画图:
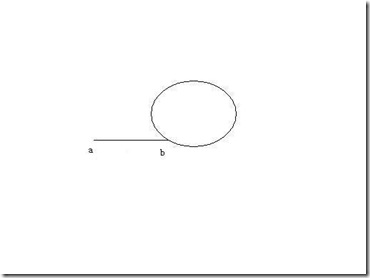
设步长分别为x和y,链表回环结点数为n,非环回环为m
设经过t次跨步,则只要xt和yt对n同余并且xt和yt都大于m就可以相遇(假设x>y)
xt-yt=pn
yt>m
得到:
t=pn/(x-y) > m/y(只需pn可整除(x-y))
指针移动次数为(x+y)t=(x+y)/(x-y)*pn
而要想pn永远整除(x-y),那么x-y=1即可。在x-y固定为1的情况下x+y越小,则移动次数越少,也即指针比较次数越少,所以x为2,y为1。
其实还有第二个问题,即,假设ptr_fast在ptr_slow走完一圈前相遇,那环的长度和链表的长度分别为多少。(注意:以下方法是有问题的,如果ab足够长的话,那可能是在好几圈之后相遇的)
我们根据第一个问题的结论,假设ptr_fast和ptr_slow在c点相遇。
图示:
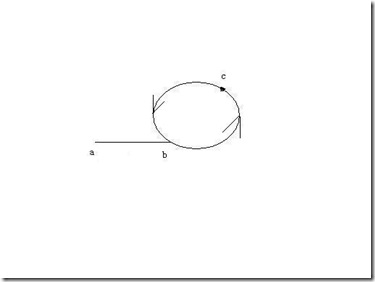
假设x是速度,t是时间。
则对ptr_slow:
ab+bc = x * t
对ptr_fast:
ab+bc+cb+bc = 2x*t
所以得出:
cb + bc = ab + bc
即:
cb = ab
所以环的长度就求出来了,即bc+cb = bc + ab = ptr_slow走的路程。
那链表的长度呢?
现在已经有了ab+bc的长度,只需要知道ab或者cb的长度即可:
再创建一个指针ptr_new,让ptr_new从head开始,和ptr_slow同时开始走,都是每次一步,由于ab == cb,所以他们相交的地方就是b点。所以即可得到整个链表的长度。
如果不是在慢指针走一圈内相遇,我还没有想到有算出环的长度和链表长度的方法,大家如果有答案欢迎告知~~
依云 on #
这办法不错啊
Reply
Dante on #
呵呵,不知道是哪位数学达人想出来的,的确很是巧妙~
Reply
熊猫 on #
恩,看来简单的方法未必是最好的
Reply
Code之行人 on #
仅仅访问会弄脏数据?但是第二种方法也访问链表啊
Reply
Dante on #
呃,不是这个意思,如果一个指针的话,你需要记录自己走过的足迹,才能知道自己是不是走到已经走过的路上了。
如果不想弄脏数据的话,就需要单独的容器来存储走过的节点的指针,但这样就会增加查找的成本。
Reply
奇怪 on #
我想问的是为什么相遇的时候满足ab+bc+cb+bc = 2x*t ,而不是ab+bc+cb+bc+cb+bc+... = 2x*t
??????
Reply
Dante on #
是我搞错了。。。
的确,如果ab足够长的话,那可能是在好几圈之后相遇的。。
多谢指出。
Reply
BBB on #
不管ab多长都是一样的,因为ab上多走多少,圈上就会少走多少啊
Reply
Mr.Bear on #
第一种方法的话,为什么要记录自己走过的所有的足迹呢。
弄2个指针,一个不动,一个往前走。
每走一步比较两个指针的值。
如果出现相同值那链表就是环状的。
如果往前走的那个遇到了NULL,那就不是的呗。
如果非环状链表的最后一个元素中指向下一个元素的指针不是NULL,那链表的生成方法上就出了问题。
不知道我的看法有没有漏洞?
Reply
Mr.Bear on #
看了博主的图示,我明白了。
是验证一个链表的一部分有环,而不是从头到尾连起来的完整的环形链表。
Reply
hexie on #
to 如果不是在慢指针走一圈内相遇,我还没有想到有算出环的长度和链表长度的方法.
i)
定义一对快慢指针分别为ptr_fast,ptr_slow,ptr_slow走一步,ptr_fast走两步,如果ptr_slow和ptr_fast最终能相遇,那么证明有环.
假设x是速度,t是时间。
则对ptr_slow:
ab+bc = x * t
对ptr_fast:
ab+M*(bc+cb)+bc = 2x*t
所以得出:
M*(bc+cb) = ab + bc
即:
ab=cb+(M-1)*(bc+cb)
ptr_slow= bc + ab=L1
ii)
再创建一个指针ptr_new,让ptr_new从head开始,和ptr_slow同时开始走,都是每次一步,由于ab == cb+(M-1)*(bc+cb),所以他们相交的地方就是b点。定义一个指针pp=点C所在位置指针。ptr_slow在围绕环转圈的过程中会和PP相遇M-1次(初始二者处于同一位置不计)。
得出M值
M=m。
此时
ptr_new走过的长度 ab=L2.
iii)
所以
环的长度
Ring=bc+cb = (bc + ab )/M= L1/m。
链表的长度
Link=ab+bc+cb=L2+L1/m.
Reply
signifox on #
to 如果不是在慢指针走一圈内相遇,我还没有想到有算出环的长度和链表长度的方法.
i)
定义一对快慢指针分别为ptr_fast,ptr_slow,ptr_slow走一步,ptr_fast走两步,如果ptr_slow和ptr_fast最终能相遇,那么证明有环.
假设x是速度,t是时间。
则对ptr_slow:
ab+bc = x * t
对ptr_fast:
ab+M*(bc+cb)+bc = 2x*t
所以得出:
M*(bc+cb) = ab + bc
即:
ab=cb+(M-1)*(bc+cb)
ptr_slow= bc + ab=L1
ii)
再创建一个指针ptr_new,让ptr_new从head开始,和ptr_slow同时开始走,都是每次一步,由于ab == cb+(M-1)*(bc+cb),所以他们相交的地方就是b点。定义一个指针pp=点C所在位置指针。ptr_slow在围绕环转圈的过程中会和PP相遇M-1次(初始二者处于同一位置不计)。
得出M值
M=m。
此时
ptr_new走过的长度 ab=L2.
iii)
所以
环的长度
Ring=bc+cb = (bc + ab )/M= L1/m。
链表的长度
Link=ab+bc+cb=L2+L1/m.
Reply
ponyma on #
如果不是在慢指针走一圈内相遇,我还没有想到有算出环的长度和链表长度的方法
~~~~
建议楼主再想想 :>
http://hi.baidu.com/ixjtu/blog/item/ef4addb59e758dcd37d3ca71.html
Reply
Dante on #
呃。。。你的名字。。
这题目好久了。。当时想的头大。。
Reply
shen on #
快指针速度是慢指针的两倍,第一次相遇一定是在慢指针刚进入环的第一圈内
Reply
clar on #
1. 快指针(2步/次),慢指针(1步每次)。如果相遇,相遇点必然在环内。当慢进入环后,依据相对速度,必然在一圈内相遇。假设相遇时间t1
2. 相遇后, 固定快指针,继续慢指针,假设t2时间后,再相遇。则环长度 = t2,固定满指针。
3. 而我们知道t1 必然是 t2的倍数,假设n倍,因为在第一次相遇时, 快指针比满指针多走了n圈(n>=1)
4. 从头再创建一个慢指针,并步进t2*(n-1),这个时侯再同时步进原先的慢指针,直至相遇,设时间t3.
则链长t1+t3
Reply
lltg on #
^p ^q两指针,
令p q=头 第一轮p走1格判nil判=q
均不等则令q=p 第二轮p走2格每次判nil判q
……
第n轮p走2^(n-1)格
复杂度O(n) 环长度=这轮中p走距离。
Reply
xavier on #
上面所有的做法应该都是错的。。。。
即使是ponyma先生给的那个链接里的推导似乎也是没有解决问题:
“可以得出 N0 = K*R+X ,K为非负整数
接下来那就怎么怎么就行了 ” 这里的X依然是未知数。
继续博主的模型(a,b,c)
当快指针追上慢指针时(c点),指针所指的位置肯定是在环内,在c点把环切开。形成两条有公共点的链表(abc,cbc'),依次遍历abc, cbc'。设得到链表的长度尾m, n。
继续从两链表表头开始遍历, 如果m>n, 遍历abc的指针先走m-n步。然后遍历两个链表的指针同时向前走,每走一步比较以下是否相同,如果相同即为b点。找到了b点,其他要求的就都可以求解了。
该时间复杂度依然是o(n)。当然还要记得修补好切开的链表。
Reply
X on #
不用切开/修复操作 记录c点(作为一个逻辑上的NULL) 再从c点出发遍历环 如果next==我们记录的‘NULL’点 就是环的长度 其他操作类似
Reply
X on #
我是褒义
Reply
X on #
这算法非常浪漫啊 我是褒义
Reply
cc on #
当慢指针进入环瞬间,慢指针位置为PPS,此时快指针位置为PPF
非环长度L0=PPS-0
此时指针相距L1=PPF-PPS
然后走 t 步后让两个指针相交
环长度L2=t+L1
链表长度L=L0+L2
有什么方法判断慢指针进入环瞬间?
Reply
shen on #
第一次与第二次相遇之间的路程就是环的长度
Reply
晓 on #
太奇妙了 数学!
Reply